Exercices dapplication du module 2

Exercice 1

Pour capter un signal électromagnétique, on utilise une antenne dont la dimension est proportionnelle au quart de la longueur d'onde.

Lorsqu'une antenne est placée dans un champ électromagnétique, une force électromotrice induite fait circuler un courant dans le circuit LC placé à sa base.

1) Calculez l'équation représentant la tension aux bornes de LC en fonction de i.

2) On suppose que i=I cos(2 pi f t), avec f=220 kHz, et la capacité C=410 pF. Calculez L pour accorder le circuit sur la fréquence porteuse.

Exercice 2

PARTIE 1

On rappelle qu’un signal AM avec porteuse a pour expression :

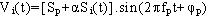
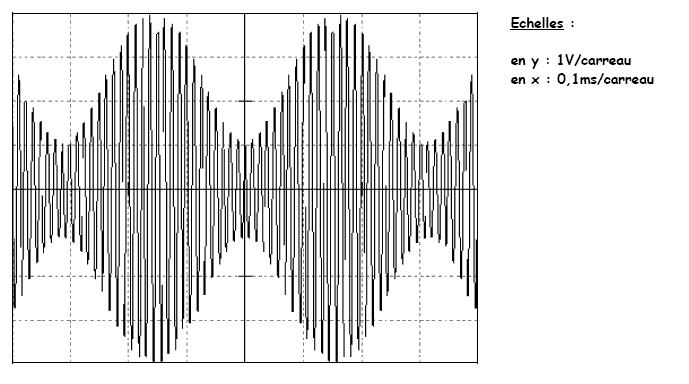
Le signal modulant est sinusoïdal. On note Si(t) = acos(Ωt), le signal de fréquence F. On présente un enregistrement de la porteuse modulée sur la courbe ci-dessous :

1) Donnez l’expression littérale de la porteuse e(t) modulée par un signal basse-fréquence sinusoïdal et rappelez la définition de l’indice de modulation m.
2) A partir de l’enregistrement fourni, déterminez les valeurs des fréquences f de la porteuse et F du signal modulant.
3) A partir de la même courbe, déterminez la valeur de l’indice de modulation m et de l’amplitude de la porteuse E.
4) Tracez l’allure du spectre de ce signal et en déduire l’encombrement spectral de ce signal modulé.

PARTIE 2

On rappelle qu’un signal AM avec porteuse a pour expression : e(t) = E(1 + k.s(t)).cos(ωt)
On donne les valeurs numériques suivantes :

• fréquence de la porteuse f = 1 MHz
• amplitude de la porteuse E = 10 V
• coefficient k = 0,1
• signal modulant sinusoïdal s(t) = 5cos(Ωt) de fréquence F = 1 kHz

1) Donnez l’expression mathématique de e(t) et tracez son allure.
2) Quelle est la valeur de l’indice de modulation m ?
3) Représentez le spectre du signal e(t).
4) Ce signal AM est fabriqué à l’aide d’un multiplieur selon le schéma suivant :

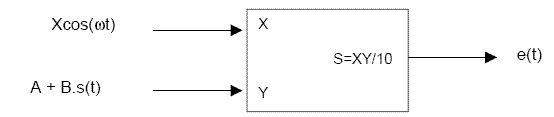
Proposer des valeurs pour A, B et X

5) On veut émettre ce signal à 27 MHz et non plus à 1 MHz. Dessinez le schéma fonctionnel complet de l’émetteur.