Démonstration
Nous avons vu en cours Système que tout signal physique possède un spectre dont le module est symétrique autour de l'axe des ordonnées, comme représenté sur la figure suivante (Figure 4). Cependant, physiquement les fréquences négatives n'existent pas et par conséquent la mesure du spectre d'un signal quelconque est représenté uniquement pour des fréquences positives.
Néanmoins, les fréquences négatives existent en théorie. Lorsqu'on translate le spectre autour d'une fréquence porteuse fp, on translate la totalité du spectre. On retrouve donc le spectre (mesurable) suivant (Figure 5)
Cas particulier
 Question 5
Question 5
Supposons que le message à transmettre m(t) soit un signal sinusoïdal, d'amplitude Sm et de fréquence fm . Prenons une porteuse d'amplitude A et de fréquence fp .
- Tracez le spectre M(f) du signal d'information m(t) à partir de la table des Transformée de Fourier.
- Expliquez la relation entre le spectre et la formule suivante :
| sachant |
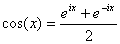 |
et |
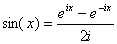 |
- A partir du théorème 4, écrire la formule mathématique du signal modulé.
- A partir des formules trigonométriques suivantes, simplifiez l'expression pour ne plus avoir que des sommes de sinus et de cosinus (on supprime les produits de cosinus).
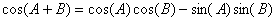
(pour les plus courageux, démontrez cette formule à partir de l'expression donnée au 2)

