Ex 1: Le décibel.
| G |
2 |
4 |
8 |
16 |
32 |
| GdB |
6,02 |
12,04 |
18,06 |
24,08 |
30,10 |
On remarque que lorsque le gain linéaire double, le gain en décibel augmente de 6,02 db.
| G |
0,1 |
1 |
10 |
100 |
1000 |
| GdB |
-20 |
0 |
20 |
40 |
60 |
On remarque que lorsque le gain linéaire est multiplié par 10, le gain en décibel augmente de 20 db.
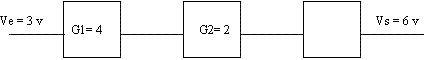
- Le gain total G = vs/ve = 6/3 = 2
- G1dB = 20 log G1 = 20 log 4 = 12,04 dB
- G2dB = 20 log G2 = 20 log 2 = 6,02 dB
- La tension en sortie du premier étage vs1 = G1 * ve = 4 * 3 = 12 v; la tension en sortie du deuxième étage vs2 = G2 * vs1 = 2 * 12 = 24 v; donc le gain du troisième étage G3 = vs/vs2 = 6/24 = 0,25 v soit en décibel G3dB = 20 log G3 = -12,04 dB
- Le gain total en décibel GdB = 20 log 2 = 6,02 dB
- On remarque donc que l'on a bien GdB = G1dB + G2dB+ G3dB, alors qu'en échelle linéaire G = G1*G2*G3
Ex 2 : Le dBm.
| P(mW) |
0,1 |
0,25 |
0,5 |
1 |
2 |
| P dBm |
-10 |
-6,02 |
-3,01 |
0 |
3,01 |
Un système reçoit en entrée une puissance de -6 dBm, cela correspond à une puissance Pe = 10 exp ( -6/10 ) *1 mW= 0,25 mW. Un gain de 6 dB revient à une amplification de G = 10 exp ( Gdb/10) = 4 donc la puissance de sortie du système est Ps = 4 * Pe = 1 mW soit en dBm, PsdBm = 0 dBm
On remarque donc que le calcul aurait été plus rapide avec les dB :
PsdBm = Gdb + PedBm
Ex 3 : Atténuation
Un signal d'entrée d'amplitude +25 volts représentant un "0", sera bien reçu par le récepteur si en sortie de ligne sa tension reste supérieure à +3 volts. Il peut donc subir une atténuation maximale Amax = 25/3 = 8,33 soit 18,4 dB.
On souhaite que l'atténuation du support de L mètres soit inférieure à cette atténuation maximale Amax donc : 5 * L < AdBmax d'ou L < 368 m

