Les travaux pratiques proposés ici sont à réaliser sous le logiciel de simulation et de calcul Matlab.
TP1 : Décomposition en série de Fourier
- Ecrire un programme utilisant une boucle ‘for' qui trace deux périodes du signal rectangulaire de fréquence 2000 Hz dont la décomposition en série de Fourier est donnée ici :
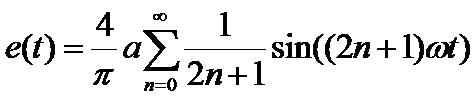
L'indice n sera passé en paramètre au programme ( fonction « input »), l'axe des temps sera
t = 0:1/1000000:1/1000 ;
- Pour n = 3, n=6, n=12 afficher l'allure du signal temporel. Comment s'appelle ce signal ? Que se passe t il quand n augmente ? Quel indice n minimum donne une bonne idée de l'allure du signal.
- La fonction spectre(t,y) trace le spectre d'un signal ‘y', calculé sur un vecteur de temps t. Cette fonction est disponible ici
 , mettez la dans votre dossier avec les scripts Matlab. Une analyse spectrale devant se faire sur une durée théoriquement infini, on multipliera par 10 la valeur finale de t. Utilisez cette fonction dans votre programme pour afficher le spectre du signal sur un deuxième graphe ( figure(2) ).
, mettez la dans votre dossier avec les scripts Matlab. Une analyse spectrale devant se faire sur une durée théoriquement infini, on multipliera par 10 la valeur finale de t. Utilisez cette fonction dans votre programme pour afficher le spectre du signal sur un deuxième graphe ( figure(2) ).
- Pour les valeurs de n = 3, 6 donner la bande passante du signal.
- Comparez le spectre théorique ( spectre de raies ) de ce signal et le spectre réel, donnez une interprétation du phénomène.
TP2 : Le signal porteur d'information
La numérotation téléphonique DTMF associe à chaque chiffre du cadran du téléphone, un couple de fréquences dans la bande passante audible. Le signal généré est alors la somme de deux signaux sinusoïdaux à ces deux fréquences.
| fréquences en Hz |
1209 |
1335 |
1477 |
1633 |
| 697 |
1 |
2 |
3 |
A |
| 770 |
4 |
5 |
6 |
B |
| 852 |
7 |
8 |
9 |
C |
| 941 |
* |
0 |
# |
D |
- Ecrire un script qui représente le signal sur la ligne lorsque l’on appui sur un chiffre passé en paramètre au programme ( fonction input ). On utilisera l’instruction if, elseif, end pour tester la valeur entrée. Pour définir l’axe des temps on utilisera les variables et les valeurs suivantes afin de respecter les contraintes sur les signaux numériques (Shannon)
tf=1/20;
pas=tf/1000;
t=0:pas:tf;
- Pour chaque touche de 0 à 9 précisez si le signal est périodique et relevez sa période.
- La fonction sound de matlab permet de diriger le signal vers la carte son. Pour écoutez votre signal il faut augmenter sa durée : fixez tf à ½ et remplacez l’affichage par : sound(s,1/pas), qu’entendez vous ?
- Utilisez la fonction spectre, pour afficher le spectre du signal correspondant à chaque touche du téléphone. Relever à chaque fois la bande passante. Conclure sur l’intérêt de cette représentation de l’information.
- A l’autre de bout de la ligne téléphonique l’autocommutateur va devoir interpréter le signal pour vous mettre en relation avec votre correspondant, proposez un dispositif qui soit capable d’identifier les fréquences.
- Complétez votre scripte pour composer un no à deux chiffres. On pourra utiliser un vecteur et une boucle ‘for’ par exemple. Fixez le pas à tf/10000.
- Testez en apposant un combiné téléphonique sur le haut parleur de votre ordinateur.
TP3 : Systèmes de filtrage
Comprendre les effets d’un système de filtrage à partir de l’observation des grandes familles de filtres. On utilisera le module simulink de matlab.
Ouvrir un nouveau document simulink dans lequel on placera un générateur de signal, un filtre de Chebychev passe bas de type I ( bloc extra, filters, Analog lowpass ) et un graphe plus un multiplexeur pour afficher deux courbes sur le même graphe.
Pour analyser les spectres, on va rediriger l’entrée et la sortie du filtre, dans des variables de l’interpréteur de commande, avec le bloc toworkspace. Ensuite la fonction spectre() affiche des spectres de meilleur qualité que le bloc analyseur de spectre. Il faut aussi rediriger l’horloge avec autre bloc toworkspace et un bloc clock.
Réaliser le montage pour que l’on puisse afficher le signal avant et après filtrage sur le même graphe.
Régler :
- La simulation en Linsim. ( max step size = 10 -6 ; min step size = 10 -6 ).
- La fréquence de coupure pour le filtre à 59 kHz , un ordre 2 et 3 db d’oscillations dans la bande passante.
- Le générateur de signaux avec un signal rectangulaire à 20 kHz d’amplitude 1 volt.
- Le Stop Time en cohérence avec le graphe pour afficher quelques périodes du signal.
Remarque : les fréquences sont à donner en rd/s conformément à la notation anglo-saxonne.
Lancer la simulation et commentez l’effet du filtre sur le signal temporel et sur le signal fréquentiel.
- Que devrait on voir avec un filtre idéal ?
- Augmenter progressivement l’ordre du filtre ( 5, 10, 30 ), que se passe-t-il ?
- Echanger le filtre de Chebychev par un filtre de Butterworth. A même ordre, lequel vous semble avoir la coupure la plus raide ? ( prenez un ordre assez élevé pour voir les différences! )
- Placer en série un filtre passe bas de Butterworth de coupure 59 kHz et un passe haut de Butterworth de coupure 59 kHz d'ordre 30. Que devrait on obtenir si les filtres étaient idéaux ? Quel filtre a t on ainsi réalisé ? justifiez.
- Envoyer un bruit d'ampplitude 0,5 v avec un signal sinusoïdal d'amplitude 1v à 20 kHz. Filtrer en passe bas à 20 kHz. Affichez le signal temporel avant et après filtrage ainsi que les spectres. Quel est l’effet du filtre sur le rapport signal à bruit ?

