1°) Le programme est le suivant :
clear
t=0:1/100000:1/1000;
n=input( 'Valeur de n ? ' ); %On demande l'indice n %
s=0;
for i=0:n; %boucle : i varie de 0 à n%
f=(4/pi)*(1/(2*i+1))*sin(4000*pi*(2*i+1)*t);
s=s+f;%On place le résultat de f dans s, en l'ajoutant à l'ancien résultat de s%
end %fin de la boucle%
plot(t,s); %on trace le graphique%
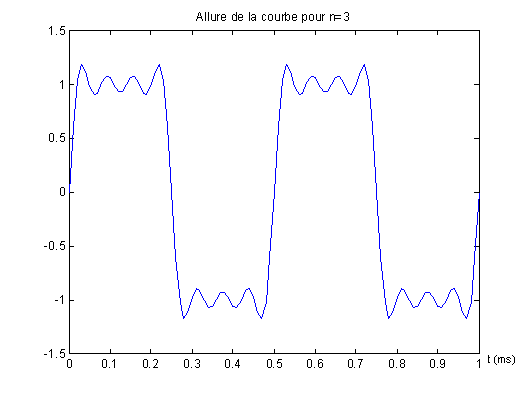
2°) Résultat du script pour n = 3
-
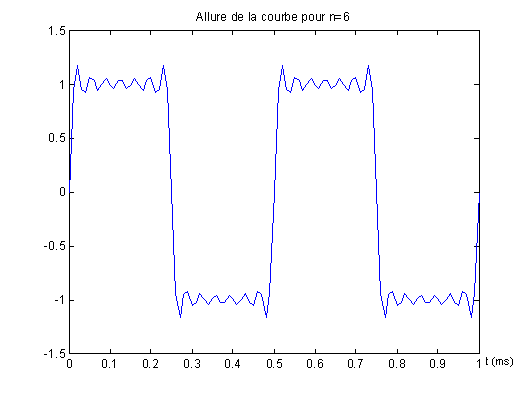
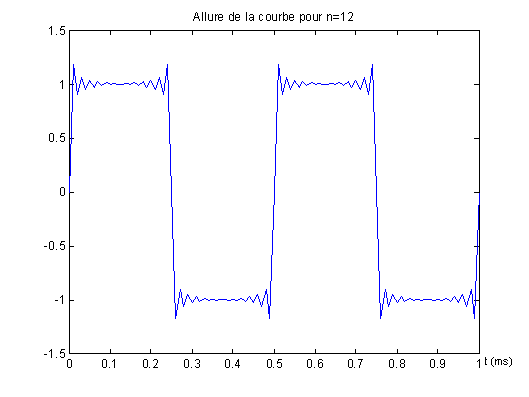
Dans les trois cas on obtient un signal périodique de période 0,5 ms, le nombre d'ondulations -1 correspond au nombre d'harmoniques du signal.
- Plus l'indice n augmente, plus les ondulations sont faibles et plus on tend vers un signal rectangulaire. En théorie il fatu un indice n infini pour construire le signal rectangulaire à partir de la somme de signaux sinusoïdaux.
- En pratique, dès n=3 on est très proche des caractéristiques du signal rectangulaire : amplitude +1 ; -1 et fréquence 2000 Hz.
3°) Le script pour afficher le spectre devient :
clear
t=0:1/100000:1/100; %on multiplie par 10 la durée de la simulation
n=input('Valeur de n ? '); %On demande l'indice%
s=0;
for i=0:n;
f=(4/pi)*(1/(2*i+1))*sin(4000*pi*(2*i+1)*t);
s=s+f;
end
spectre(t,s);
On obtient pour n=3 :
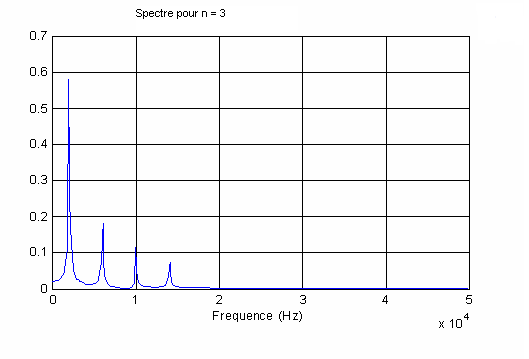
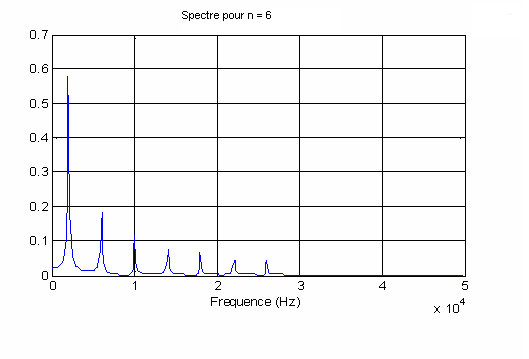
4°) Pour n = 3 on relève une bande passante de 14 kHz et pour n = 6 la bande passante est de 26 kHz. ce qui est cohérent puisque fn = (2*n+1)*2000 Hz.
5°) On remarque que le spectre affiché n'est pas tout à fait un spectre de raies, l'énergie s'étale autour d'une valeur maximale de la fréquence, cela est du au fait que l'on effectue une analyse spectrale sur une durée finie. Plus on augmente la durée de l'analyse et plus le spectre va tendre vers un spectre de raies.

