Ex 1 : Filtrage idéal.

Le signal rectangulaire d'amplitude 3 v et de fréquence 4 kHz vu lors de l'exercice 1 du chapitre 9 avait le spectre suivant :

Le filtre passe bande idéal de bande passante [5kHz ; 13 kHz] a le gabarit suivant :

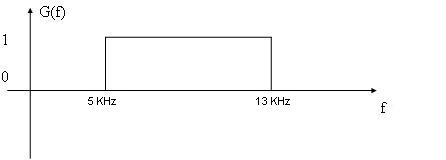
Donc seule la raie à 12 KHz est conservée, d'ou le spectre du signal de sortie :

Le signal de sortie est donc un signal sinusoïdal d'amplitude 1,27 volt et de fréquence 12 kHz qui s'écrit : s(t) = 1,27 sin (2*12000*pi*t).

Ex 2 : filtre passe bande.

X(t) est un signal somme de signaux sinusoïdaux, son spectre est donc composé de raie aux fréquences 1000, 2000 et 3000 Hz, d'amplitude 4, 2 et 1 volts.

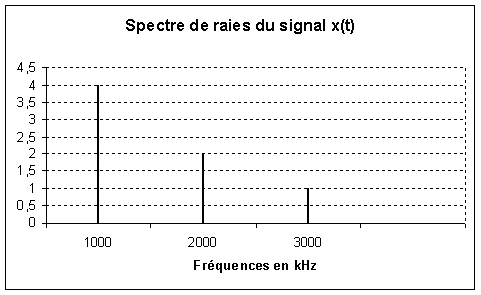
Sur la courbe de gain on relève que pour 1000 Hz le gain est de 1, pour 2000 Hz le gain est de 0,5 et pour 3000 Hz le gain est nul.

Sur la courbe de phase on relève que pour 1000 Hz le déphasage est de 0°, pour 2000 Hz le déphasage est de 90°, et pour 3000 Hz le déphasage est de 90°.

Le spectre du signal de sortie est donc :

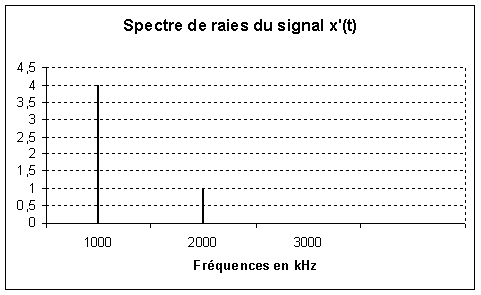
Le signal x'(t) a donc pour équation : x'(t) = 4 sin ( 2000 pi t) + sin ( 4000 pi t + pi/2)

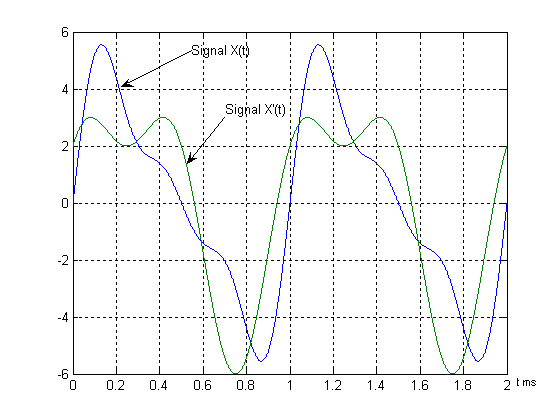
On remarque que le filtre a profondément modifié l'allure temporelle du signal en apportant un déphasage et une atténuation.