Exercice 1 :
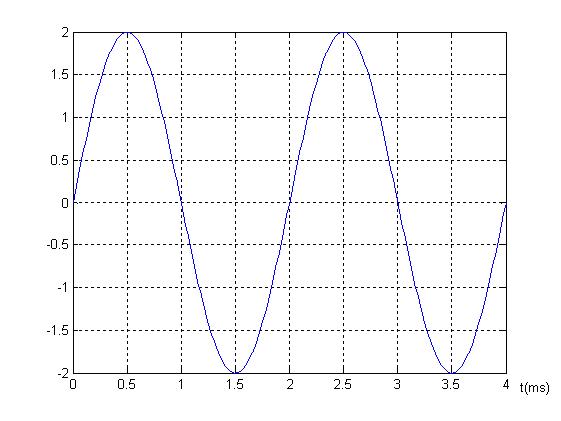
La fréquence est l’inverse de la période donc 1/0,002 = 500 Hz
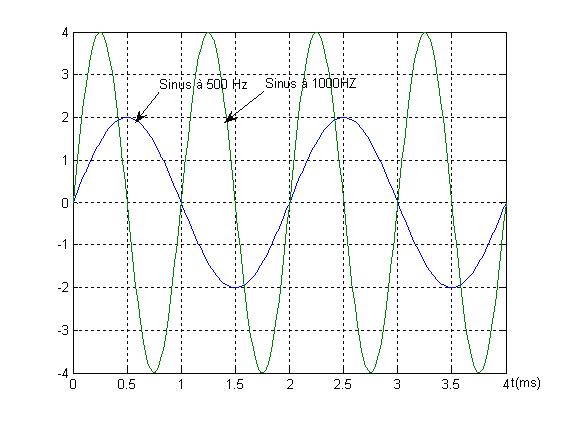
Les équations des deux signaux sont:
- signal à 500 Hz : Y1 = 2*sin(1000*pi*t)
- Signal à 1000 Hz : Y2= 4*sin(2000*pi*t)
Exercice 2 :
Le retard d’un signal sinusoïdal déphasé est :
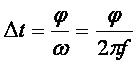
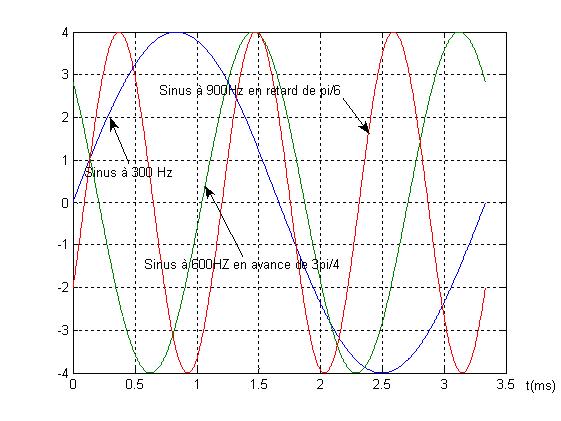
Le sinus à 600 Hz est en avance de 3/8*600 = 0,625 ms
Le sinus à 900 Hz est en retard de 1 /(6*900) = 0,0926 ms
Exercice 3 :
Valeur moyenne de S1 = 1/T * ( -A/2 * T/2 *1/2 + A/2 * T/2 * 1/2) = 0 ;
Valeur moyenne de S2 = 1/T * ( A/2 * T/4 *1/2 - A/2 * T/4 *1/2 - A/2 * T/4 *1/2 + A/2 * T/4 *1/2 ) = 0;
Valeur moyenne de S3 = 1/T * ( A * T/2 - A/2 * T/2 ) = A/4;
Valeur moyenne de S4 = 1/T * ( 1/2 * A * T ) = A/2;
Valeur moyenne de S5 = 1/T * ( A * T/3 - A * 2*T/3 ) = -A/3;
On remarquera en comparant S1 et S4 que si l'on retire à un signal périodique sa valeur moyenne on obtient un signal centré sur 0. Autrement dit un signal périodique peut se décomposer en une valeur moyenne plus un signal centré sur 0.

