Exercice 1 : Signal rectangulaire
1°) On identifie le terme d'amplitude des signaux sinusoïdaux : Cn = 4.a/(2n+1).pi et le terme des fréquences : Wn = (2n+1)w d'où Fn = (2n+1).F
Pour n = 0 on obtient un signal sinusoïdal de fréquence F c'est donc le fondamental puisque sa fréquence est identique à celle du signal périodique. L'amplitude du fondamental est alors de 4.a/pi soit 3,82 volts.
2°) Pour n = 1 on obtient un signal sinusoïdal de fréquence 3*F soit 12 kHz. C'est le premier harmonique du signal rectangulaire. Son amplitude est alors de 4.a/3.pi soit 1,27 volts.
3°) Pour n = 2 on obtient un signal sinusoïdal de fréquence 5*F soit 20 kHz. C'est le deuxième harmonique du signal rectangulaire. Son amplitude est alors de 4.a/5.pi soit 0,764 volts.
4°) Représentons le signal rectangulaire et ses harmoniques sur un même graphe
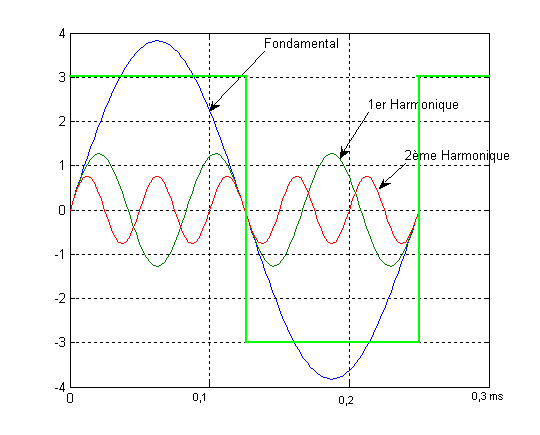
Le graphe amplitude - fréquence est plus synthétique :

Exercice 2 :
Pour le premier spectre :
- La valeur moyenne est nul, pas de raie en 0 Hz.
- Le fondamental à une amplitude de 5 volts et une fréquence de 1000 Hz
- Il y a ensuite 4 harmoniques de fréquences 2000 Hz, 3000 Hz, 4000 Hz et 5000 Hz. Les amplitudes respectives sont 3volts, 2volts, 1 volt et 0,5 volts.
- S(t) = 5 sin (2000.pi.t) + 3 sin ( 4000.pi.t) + 2 sin ( 6000.pi.t) + sin ( 8000.pi.t) + 0,5 sin ( 1000.pi.t)
- La bande passante va de 1000 à 5000 Hz, sa largeur est donc de 4000 Hz.
Pour le deuxième spectre :
- La valeur moyenne est 5 volts ( raie en 0 Hz ).
- Le fondamental à une amplitude de 3,5 volts et une fréquence de 2000 Hz
- Il y a ensuite 2 harmoniques de fréquences 4000 Hz et 6000 Hz. Les amplitudes respectives sont 2 volts et 2,5 volts.
- S(t) = 5 + 3,5 sin ( 4000.pi.t) + 2 sin ( 8000.pi.t) + 2,5 sin ( 12000.pi.t)
- La bande passante va de 0 à 6000 Hz, sa largeur est donc de 6000 Hz.
Exercice 3 :
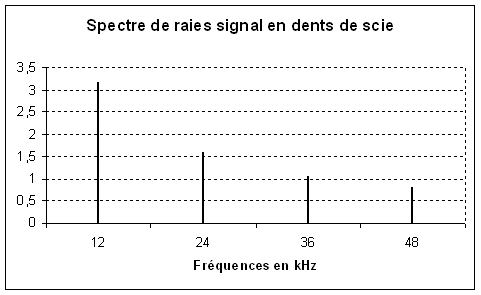
Signal en dent de scie :
| |
n |
1 |
2 |
3 |
... |
| Fréquences |
n*f |
12 kHz |
24 kHz |
36 kHz |
... |
| Amplitudes |
2.A/n.pi |
3,18 v |
1,59 v |
1,06 v |
... |
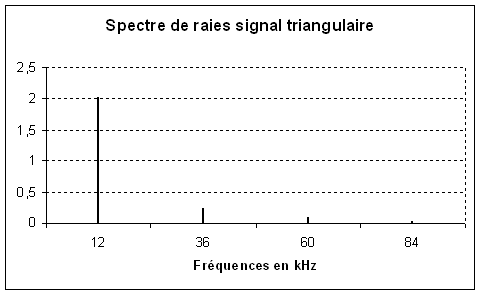
Signal triangulaire :
| |
n |
0 |
1 |
2 |
... |
| Fréquences |
(2n+1)*f |
12 kHz |
36 kHz |
60 kHz |
... |
| Amplitudes |
4.A/((2n+1).pi)2 |
2,03 v |
0,23 v |
0,08 v |
... |
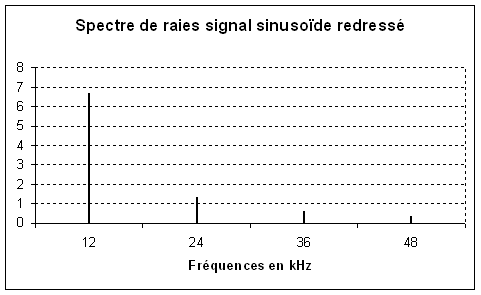
Signal sinusoïdal redressé :
| |
n |
1 |
2 |
3 |
... |
| Fréquences |
n*f |
12 kHz |
24 kHz |
36 kHz |
... |
| Amplitudes |
4.A/(4n2-1) |
6,67 v |
1,33 v |
0,57 v |
... |
On remarquera la similitude de certains spectres, qui correspondent à des signaux très différents :
- Le signal "sinusoïde redressé" possède les mêmes fréquences que le signal en dent de scie, mais pas les mêmes amplitudes.
- Les signaux triangulaire et dent de scie qui se ressemblent temporellement n'ont pas du tout les mêmes fréquences.
Le spectre d'un signal est unique.

