Formule de Bessel

cos[x.sin(2πf₀t)]=J₀(x)+2J₂(x).cos(2.2πf₀t)+2J₄(x)cos(4.2πf₀t)+...

sin[x.sin(2πf₀t)]=2J₁(x)+2J₃(x).sin(2πf₀t)+2J₅(x)2cos(5.2πf₀t)+...

La fonction cos(x.sin(2πf₀t)) s'écrit donc comme une somme infinie de cosinus. Si a représente une fréquence, on voit apparaître tous les harmoniques paires, pondérées par un facteur de Bessel, nommé J.

Pour calculer les coefficients J_k(x), on se ramène à l'abaque suivante. Celle-ci représente les 5 premières fonctions de Bessel en fonction de l'amplitude x (dénommée m dans l'équation de Bessel).

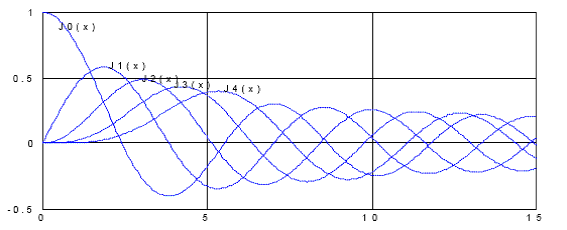
Nous étudierons un exemple au chapitre suivant. Néanmoins, l'utilisation de la formule de Bessel permet de calculer :

cos[5.sin(π/2)]=-0.2+0.04.cos(π)+0.8cos(2π)+...calculé en prenant l'amplitude de J_k(x) pour x=5