La formule de Bessel permet d'exprimer une fonction composée en sinus et cosinus sous forme de sommation de sinus et de cosinus. Cette nouvelle expression permet de déterminer le spectre du signal. Les coefficients de la formule de Bessel est exprimée en page 3.2.3. Cependant, une représentation graphique permet de déterminer les valeurs approximatives de J0(5), J1(5), …
Comparez les valeurs déterminées graphiquement à celle du tableau de la question 12.
10 - Ecrire la fonction J0(x), J1(x) et J2(x) en écrivant la somme des premiers termes.
11 - On suppose :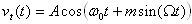 
avec m=1, et en appliquant l'équation de Bessel, on trouve :
Amplitude |
Fonction Bessel |
J0(1) |
0.765 |
J1(1) |
0.44 |
J2(1) |
0.11 |
J3(1) |
0.02 |
J4(1) |
0.002 |
Déterminez et représentez le spectre du signal.
Que signifie la valeur m=1 ?
12 - Si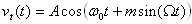 
, m=5, et que :
Amplitude |
Fonction Bessel |
J0(5) |
-0.177 |
J1(5) |
-0.132 |
J2(5) |
0.04 |
J3(5) |
0.36 |
J4(5) |
0.39 |
J5(5) |
0.26 |
J6(5) |
0.13 |
J7(5) |
0.05 |
J8(5) |
0.02 |
Déterminez le spectre du signal.
Que signifie la valeur m=5
13 - Vérifiez la règle de Carson sur les deux questions précédentes.
