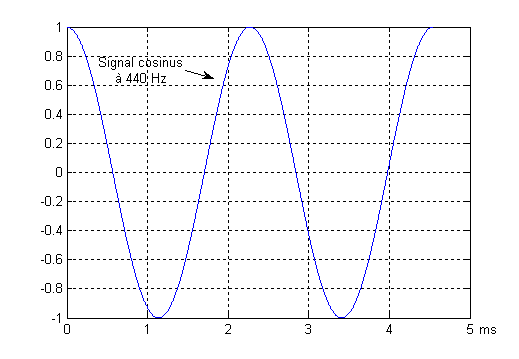
C’est le signal fondamental pour comprendre les systèmes de transmission, les signaux audiovisuels et les phénomènes physiques associés.
Expression mathématique :
s(t) = A sin( 2*pi*f*t + phi )
- f est la fréquence ( nombre de motifs par seconde ).
- La période est T = 1/f.
- La pulsation w = 2*pi*f.
- Le produit w*t est un angle en radians.
- phi est le déphasage du signal, phi/w est homogène à un temps et traduit donc le retard ou l'avance du signal.
Valeurs remarquables :
| t |
0 |
T/12 |
T/8 |
T/6 |
T/4 |
T |
| sin(w*t) |
0 |
1/2 |
0,707 |
0,85 |
1 |
0 |
Ce signal est bien réel, écoutons le  .C' est un signal sinusoïdal de fréquence 440 Hz. C'est le signal utilisé pour la tonalité de la ligne téléphonique.
.C' est un signal sinusoïdal de fréquence 440 Hz. C'est le signal utilisé pour la tonalité de la ligne téléphonique.
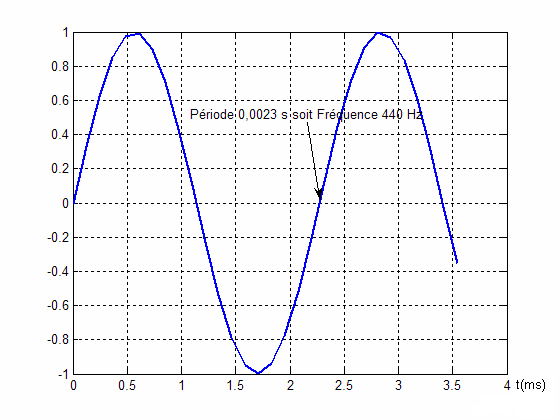
Soit le motif de couleur suivant, on remarqu'il est périodique, il correspond en fait à la vue du dessus de 100 sinusoïdes mises côte à côte. L'amplitude est ensuite colorisée à partir d'une table de couleurs.
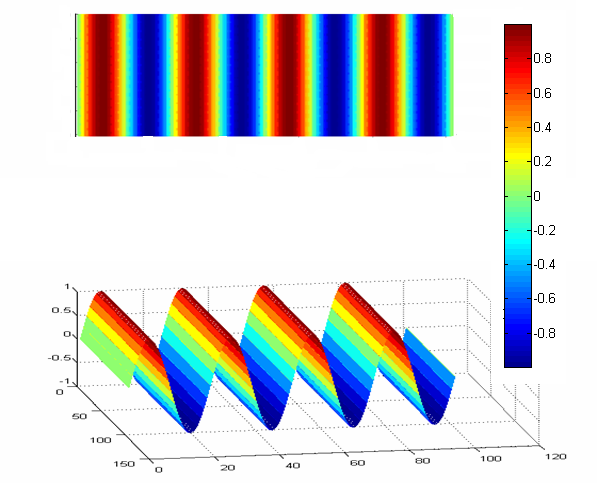
Remarque : Si l'on avance le signal sinusoïdal d'un quart de période, soit un déphasage de pi/2 on obtient un signal connu sous le nom de cosinus.
sin( 2*pi*f*t + pi/2 ) = cos ( 2*pi*f*t)