On démontre que tout signal s(t) périodique de période T peut être mis sous la forme d’une somme de fonctions sinusoïdales.
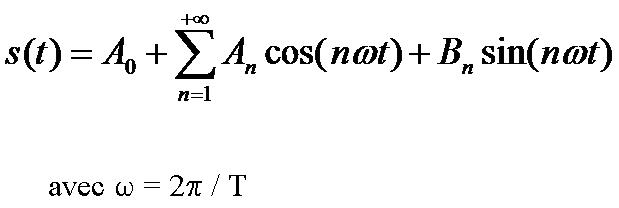

Ecriture détaillée :
s(t) = A0 + A1.cos(2.pi.F.t)+ A2.cos(2.pi.2.F.t)+ A3.cos(2.pi.3.F.t)+…+ An.cos(2.pi.n.F.t)+ …+ B1.sin(2.pi.F.t)+ B2.sin(2.pi.2.F.t)+ B3.sin(2.3.F.t)+…+ Bn.sin(2.pi.n.F.t)+ …
On peut alors représenter les différents coefficients et les fréquences associées
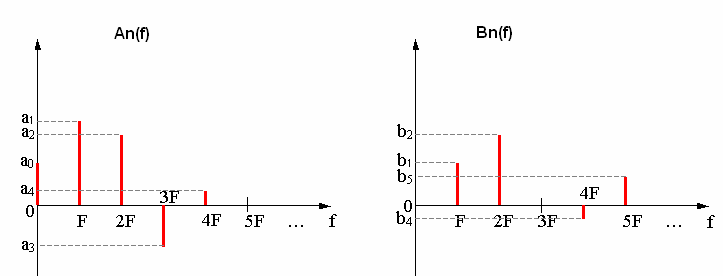
On peut encore écrire :
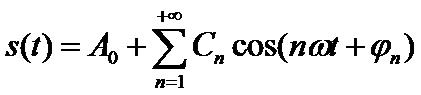
Avec
An cos (n w t ) + Bn sin (n w t ) = Cn cos ( nwt + phi n )
et phi n = Arctg (Bn / An) et Cn = ( An2 + Bn2 )1/2
Chaque terme est donc un signal sinusoïdal de fréquence n*f , et d’amplitude Cn.
On l’appelle harmonique d’ordre n du signal. On peut représenter sur un graphe l'ensemble de ces harmoniques en fonction de la fréquence.
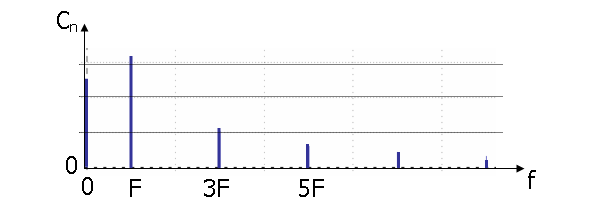
En résumé :
- Le signal s(t), périodique, se décompose donc en une somme de fonctions sinusoïdales qui sont ses harmoniques.
- Le premier harmonique est appelé le fondamental. C ’est un signal sinusoïdal de même fréquence que le signal périodique.
- Les harmoniques ont des fréquences multiples de celle du fondamental.

