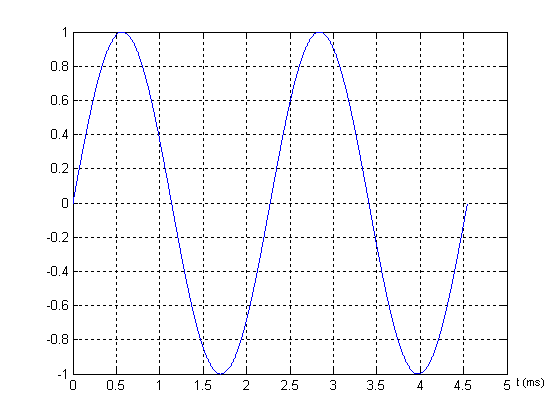
Reprenons le signal sinusoïdal de 440 Hz, d’amplitude 1 volt ( Note LA ).
S(t) = sin ( 2*440*pi*t)
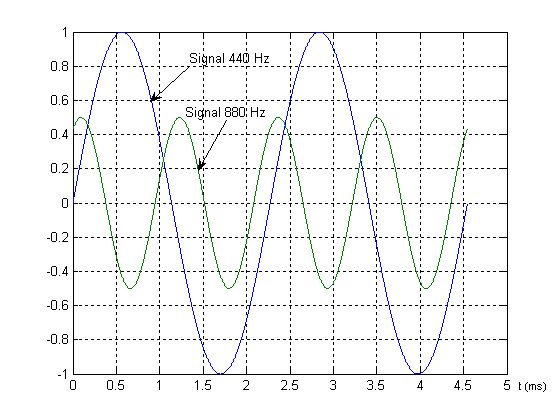
Ajoutons un deuxième signal, d’amplitude ½, de fréquence double, déphasé de 60 degrès :
S(t) = ½ *sin ( 2*pi*880*t+pi/3)
Le signal obtenu est plus petit et légèrement déphasé.
Ajoutons ainsi trois autres signaux sinusoïdaux, d’amplitude 1/3, 1/4, 1/5, de fréquence triple, quadruple et quintuple, et déphasés de 120, 180 et 240 degrés. Le signal obtenu est plus complexe mais toujours de période 440 Hz.
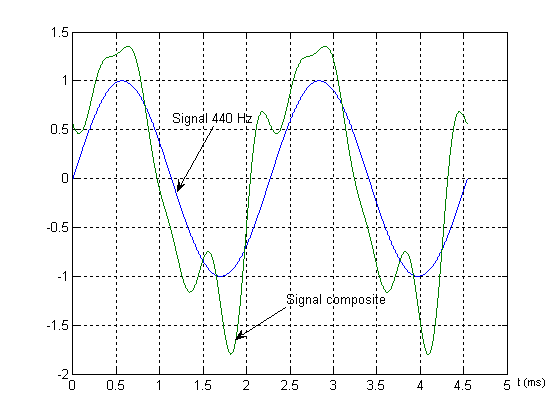
Si nous écoutons ce nouveau signal il semble plus riche en sons et sa tonalité parait plus aigu.
Son équation est plus complexe, c’est une somme de cinq signaux sinusoïdaux.
S(t)= sin(2*pi*440*t)+ ½*sin(2*pi*880*t+pi/3)+ 1/3*sin(2*pi*1320*t+pi)+ 1/4*sin(2*pi*1660*t+2*pi/3)+ 1/5*sin(2*pi*2100*t+4*pi/3)
Ce qui distingue une composante sinusoïdale d’une autre dans ce signal, c’est le couple amplitude, fréquence.
On peut représenter sur un graphe les amplitudes et les fréquences des signaux sinusoïdaux qui composent le signal. C’est ce que l’on appelle le spectre d’amplitude du signal.
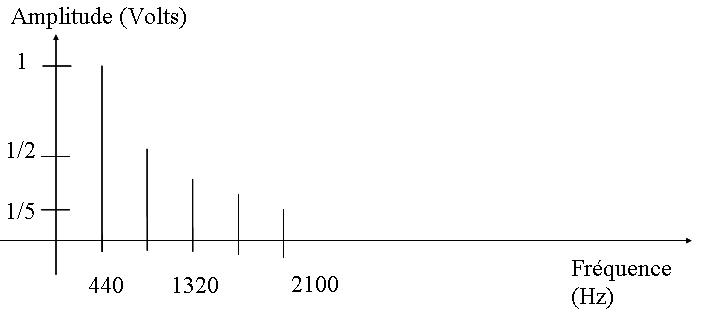
La Largeur de Bande ( ou Bande Passante) est l’intervalle de fréquences où le signal possède de l’énergie.
Dans l ’exemple la Bande Passante est comprise entre 440 et 2100 Hz, sa largeur est de 1660 Hz.
L'analyse spectrale c ’est la recherche des fréquences et des amplitudes qui composent un signal :
- Mathématiquement : en fonction de la nature du signal ( déterministe, aléatoire, périodique ), on dispose d ’un certains nombre d ’outils ( série de Fourier, transformée de Fourier ..).
- Expérimentalement : Analyseurs de spectre électronique ( pour les signaux électriques).

