On peut étendre la théorie de Fourier aux signaux non périodiques. On considère alors que les signaux non périodiques ont une période infinie.
Observons le spectre amplitude d’un signal rectangulaire dont la fréquence croît.
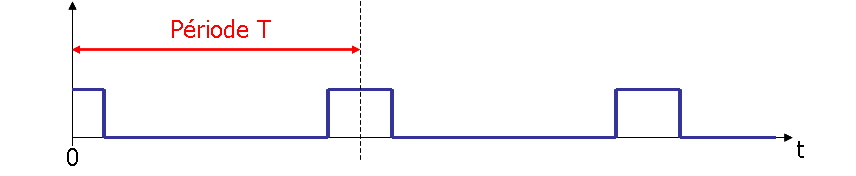
Plus T est grand plus F est petit, l'écart entre les fréquences tend vers zéro.
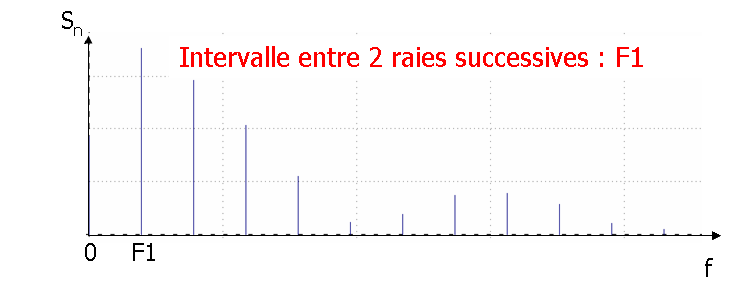

On obtient alors la densité spectrale d’amplitude d’un signal quelconque s(t) en calculant sa Transformée de Fourier grâce à la formule suivante :
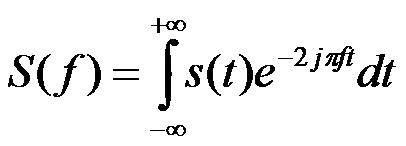
Le spectre d'un signal s'obtient alors en calculant G(f) = |S(f)|2 que l'on appelle densité spectrale de puissance.
Exemple : Soit le signal suivant, définit par l'équation simple s(t) = A pour t<T et s(t) = 0 pour t>T

Le calcul de sa transformée de Fourier nous donne une expression que l'on appelle un sinus cardinal :
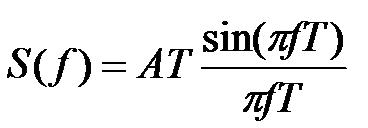
Voici l'allure du spectre correspondant dans le cas ou A = 1 et T=1/10 :
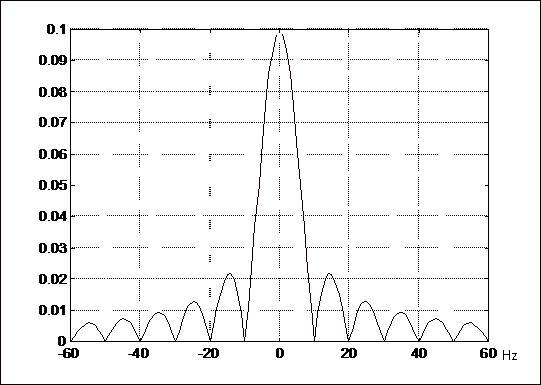
L'essentiel de l'énergie se concentre dans une bande passante = 1/T soit 10 Hz dans notre cas. On remarque que plus l'impulsion sera courte et plus la bande passante sera grande.
On retiendra que le spectre d’un signal non périodique est une courbe continue.
L’énergie d’un signal non périodique se répartit continûment sur toutes les fréquences.

